Você lança uma bola em direção a uma parede com uma velocidade de e um ângulo acima da horizontal (Fig. 4-35). A parede está a uma distância do ponto de lançamento da bola.
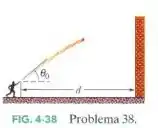
(a) A que distância acima do ponto de lançamento a bola atinge a parede?
Quais são as componentes (b) horizontal e (c) vertical da velocidade da bola ao atingir a parede?
(d) Ao atingir a parede, a bola já passou pelo ponto mais alto da trajetória?
Passo 1
Bom pessoal, o movimento como um todo pode ser dividido em dois, no eixo x temos o movimento uniforme e no eixo y temos o movimento uniformemente variado.
Vamos primeiro descobrir o tempo que a bola leva para atingir a parede:
Para calcular a altura que a bolinha atinge a parede vamos usar a equação de posição do movimento uniformemente variado:
Passo 2
A componente da velocidade no eixo x não muda pois o movimento é uniforme. Então:
Vamos agora calcular a componente de velocidade do eixo y através da equação de Torricelli:
Passo 3
Para responder o item (d) vamos lembrar que quando a bola alcança a altura máxima a velocidade em y é nula. Enquanto a bola sobe sua velocidade é positiva, ao chegar na altura máxima é nula e na descida sua velocidade é negativa.
No item anterior vimos que que é positiva, logo podemos concluir que a bola não atingiu a altura máxima.
Tranquilo, pessoal? Bora fazer mais exercícios então!!!!
Resposta
a)
b)